I’ve been extremely happy with Miro for virtual white boarding, but I always prefer open source solutions. I recently found SpaceDeck on GitHub. It’s great because it’s a nodejs application – which means I can help with it – but it’s very immature. This page will chronicle my contributions to make it better. Hopefully, in a few months I can replace Miro with SpaceDeck for professional work…
Problem One: Bad Rendering of Stars and Starbursts
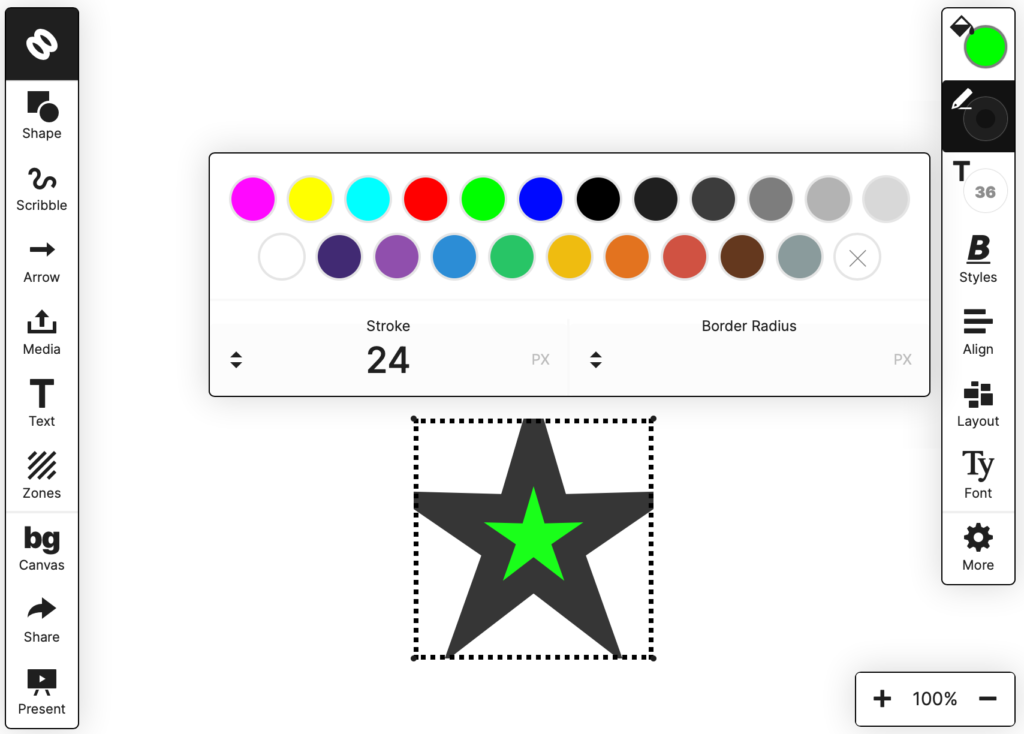
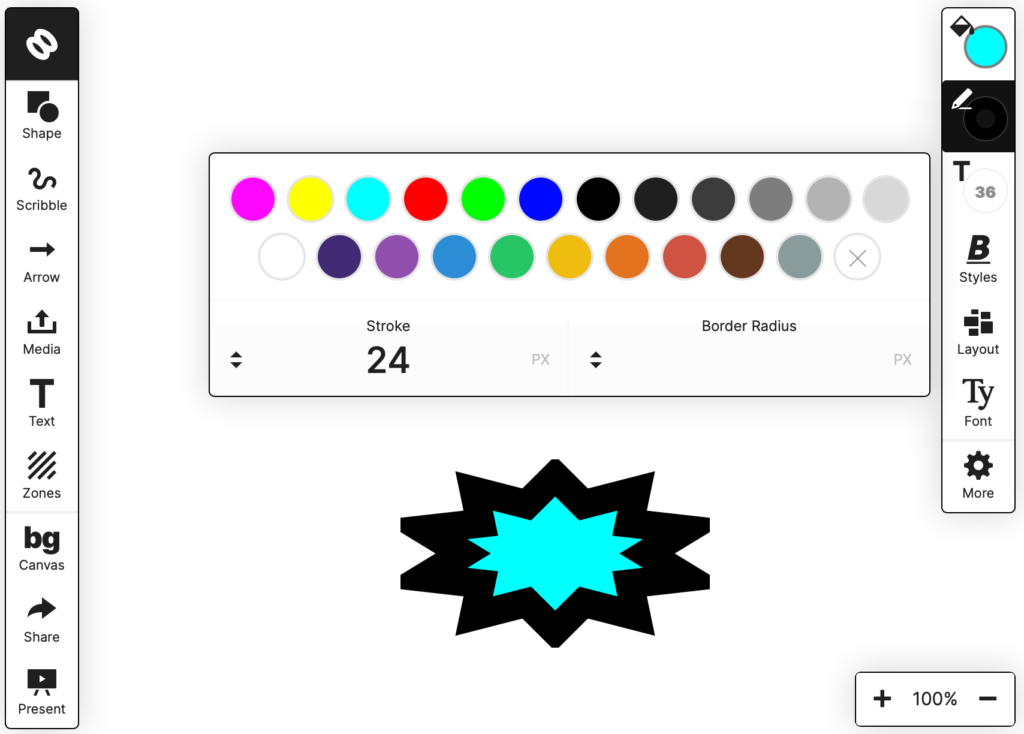
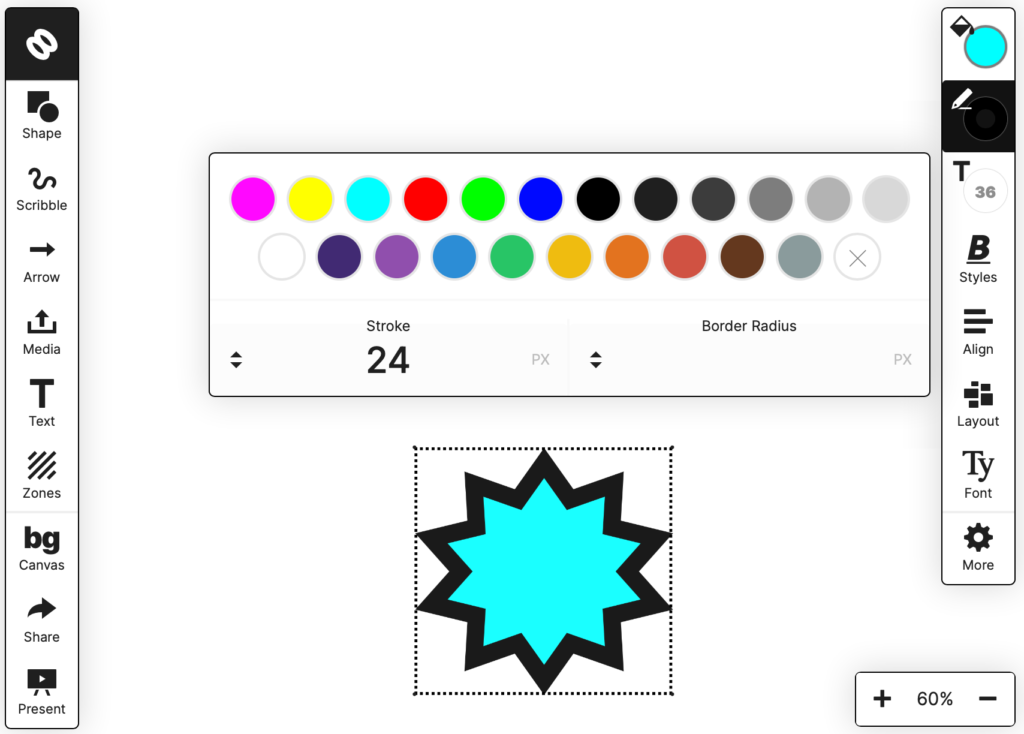
Playing with it, I noticed some problems with rendering stars illustrated by these images:
You can see that the selection box doesn’t touch the tips of the stars and that if the stroke thickness is increased, the tips are cut off!
Well, a bit of sleuthing found me the vector-render.js file was where stars are rendered… as SVG! Nice! But the algorithm for rendering them was, let’s say, naive.
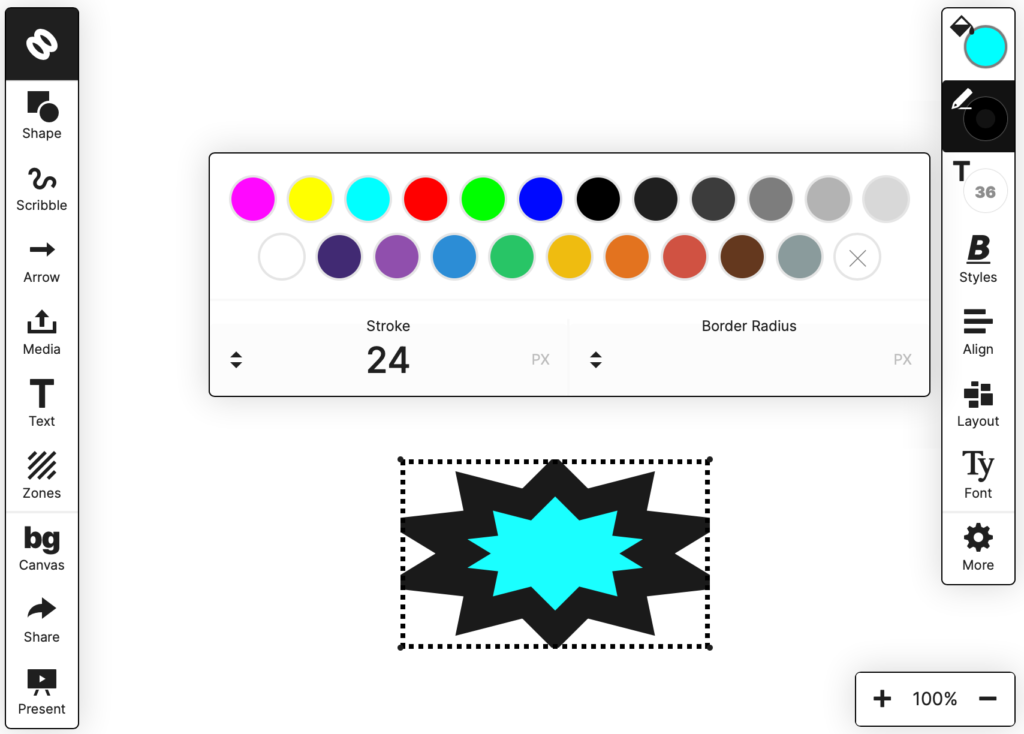
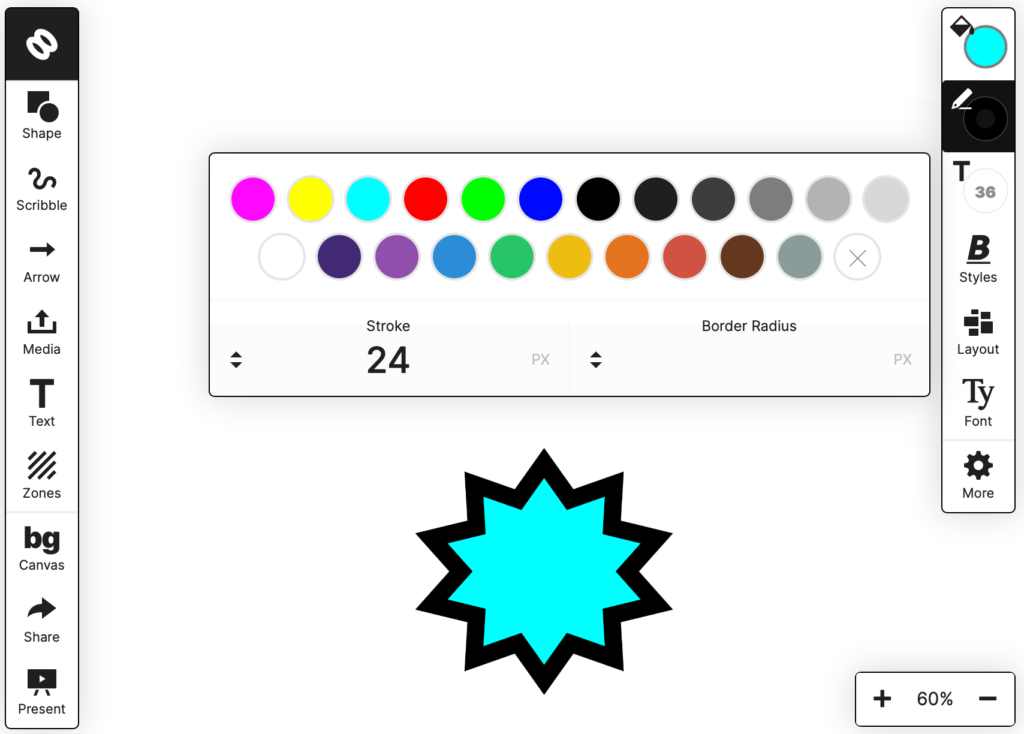
So I spent some time experimenting to see if I was in the right place… and then I started mathing! A bit of trig and vector algebra got me what I needed. Here are the results:
All told, it took me about 12 hours of work to fix this. The results are very satisfying.
Now, I gotta figure out how to contribute a “pull request” to get my fix into GitHub. I’ll update this page when I have it figured out.
My next big challenge… putting in place some unit tests for the project. I hate writing production code without unit tests! Hacking? Sure. Professional production code? No way!
For reference, here is the before and after code (sorry for the wonky text formatting):
BEFORE public/javascripts/vector-render.js:
function render_vector_star(edges,xradius,yradius,offset) {
edges *= 2;
var points = [];
var degrees = 360 / edges;
for (var i=0; i < edges; i++) {
var a = i * degrees - 90;
var xr = xradius;
var yr = yradius;
if (i%2) {
if (edges==20) {
xr/=1.5;
yr/=1.5;
} else {
xr/=2.8;
yr/=2.8;
}
}
var x = offset + xradius + xr * Math.cos(a * Math.PI / 180);
var y = offset + yradius + yr * Math.sin(a * Math.PI / 180);
points.push(x+","+y);
}
return "<polygon points='"+points.join(" ")+"'/>";
}
//....
function render_vector_shape(a) {
var stroke = parseInt(a.stroke) + 4;
var offset = stroke / 2;
var xr = (a.w-stroke) / 2;
var yr = (a.h-stroke) / 2;
var shape_renderers = {
ellipse: function() { return render_vector_ellipse(xr, yr, offset); },
pentagon: function() { return render_vector_ngon(5, xr, yr, offset); },
hexagon: function() { return render_vector_ngon(6, xr, yr, offset); },
octagon: function() { return render_vector_ngon(8, xr, yr, offset); },
diamond: function() { return render_vector_ngon(4, xr, yr, offset); },
square: function() { return "" },
triangle: function() { return render_vector_ngon(3, xr, yr, offset); },
star: function() { return render_vector_star(5, xr, yr, offset); },
burst: function() { return render_vector_star(10, xr, yr, offset); },
speechbubble: function() { return render_vector_speechbubble(xr, yr, offset); },
heart: function() { return render_vector_heart(xr, yr, offset); },
cloud: function() { return render_vector_cloud(xr, yr, offset); },
}
var render_func = shape_renderers[a.shape];
if (!render_func) return "";
return render_func();
}
AFTER:
function render_vector_star(tips,width,height,stroke) {
//A 5-pointed (5 tips) regular star of radius from center to tip of 1 has a box around it of width = 2 cos(pi/10) and height = 1 + cos(pi/5)
// assuming the star is oriented with one point directly above the center.
// So the center of the star is at width * 1/2 and height * 0.552786 which is 1 / (1 + cos(pi/5)) (also assuming the y-axis is inverted).
// The inner points are at radius 0.381966 = sin(pi/10)/cos(pi/5).
// Fortunately with simple transformations with matricies, we can do rotations and scales easily.
// See https://en.wikipedia.org/wiki/Rotation_matrix for details.
// But because the stroke is done after scaling (it's not scaled), we have to adjust the points after the rotation and scaling happens.
//A 10-pointed regular star is simpler because it is vertically symmetrical.
//NOTE: for very think stoke widths, and small stars, the star might render very strangely!
var xcenter = width/2;
var ycenter = 0;
var inner_radius = 0;
if (tips == 5) {
ycenter = height * 0.552786;
inner_radius = 0.381966; //scale compared to outer_radius of 1.0
} else { //tips == 10
ycenter = height/2;
inner_radius = 0.7; //scale compared to outer_radius of 1.0
}
// Coordinates of the first tip, and the first inner corner
var xtip = 1; // radius 1
var ytip = 0;
var xinner = inner_radius * Math.cos(Math.PI/(tips==5?5:10));
var yinner = inner_radius * Math.sin(Math.PI/(tips==5?5:10));
var points = [];
// var tmp_outside_points = []; // uncomment to see the calculated edge of the star (outside the stroke width)
var angle = 2*Math.PI / tips;
// generate points without offset from stroke width first
for (var i=0; i < tips; i++) {
var a = i * angle - Math.PI/2;
// Tip first...
// Rotate the outer tip around the origin:
var x = xtip * Math.cos(a); // because ytip = 0 we don't include: - ytip * Math.sin(a);
var y = xtip * Math.sin(a); // because ytip = 0 we don't include: + ytip * Math.cos(a);
// Scale for the bounding box:
x = x * width / (2 * Math.cos(Math.PI/10));
y = y * height / (tips==5?(1 + Math.cos(Math.PI/5)):2);
points.push([x,y]);
// tmp_outside_points.push(x+" "+y); // uncomment to see the calculated edge of the star (outside the stroke width)
// Now the inner corner...
// Rotate the inner corner around the origin:
x = xinner * Math.cos(a) - yinner * Math.sin(a);
y = xinner * Math.sin(a) + yinner * Math.cos(a);
// Scale for the bounding box:
x = x * width / (2 * Math.cos(Math.PI/10));
y = y * height / (tips==5?(1 + Math.cos(Math.PI/5)):2);
points.push([x,y]);
// tmp_outside_points.push(x+" "+y); // uncomment to see the calculated edge of the star (outside the stroke width)
}
var inset_points = [];
for (var i=0; i < points.length; i++) {
var pA = points[(((i-1)%points.length)+points.length)%points.length]; // Javascript modulus "bug"
var p0 = points[i];
var pB = points[(i+1)%points.length];
var dAx = p0[0] - pA[0];
var dAy = p0[1] - pA[1];
var dBx = p0[0] - pB[0];
var dBy = p0[1] - pB[1];
var dBLength = Math.sqrt(dBx**2 + dBy**2);
// The trig here is a bit hairy. Basically, finding the inset points is done by finding the angle (theta)
// between the tips and the neighboring inner corners (or vice versa). Then, that angle is used to
// calculate vector scaling factors for half the thickness of the stroked path. Which then is used to find
// the actual inset points for the tips and inner corners.
var theta = Math.atan2(dAx*dBy-dAy*dBx, dAx*dBx + dAy*dBy); // angle between the vectors
var theta = (i%2? Math.PI * 2 - theta : theta);
var stroke_prime = dBLength * Math.tan(theta/2); // this is really a scaling factor
var xprime = p0[0] + (i%2?-1:1)*((stroke/2)/stroke_prime)*dBx + dBy*(stroke/2)/dBLength;
var yprime = p0[1] + (i%2?-1:1)*((stroke/2)/stroke_prime)*dBy + -1 * dBx*(stroke/2)/dBLength;;
inset_points.push(xprime+","+yprime);
}
// NOTE: use svg transformations to center the thing
return "<polygon stroke-miterlimit='64' points='"+inset_points.join(" ")+"' transform='translate(" + xcenter + " " + ycenter + ")'/>";
// Append these if you want to see what is being calculated.
// The cyan dashed line is the outside of the star including the stroke width.
// The red dashed line is just the star polygon points themselves.
// "<polygon stroke-width='4' stroke='red' stroke-dasharray='16 12' fill-opacity='0' points='"+inset_points.join(" ")+"' transform='translate(" + xcenter + " " + ycenter + ")'/>" +
// "<polygon stroke-width='4' stroke='cyan' stroke-dasharray='16 12' fill-opacity='0' points='"+tmp_outside_points.join(" ")+"' transform='translate(" + xcenter + " " + ycenter + ")'/>";
}
//....
function render_vector_shape(a) {
var stroke = parseInt(a.stroke) + 4;
var offset = stroke / 2;
var xr = (a.w-stroke) / 2;
var yr = (a.h-stroke) / 2;
var shape_renderers = {
ellipse: function() { return render_vector_ellipse(xr, yr, offset); },
pentagon: function() { return render_vector_ngon(5, xr, yr, offset); },
hexagon: function() { return render_vector_ngon(6, xr, yr, offset); },
octagon: function() { return render_vector_ngon(8, xr, yr, offset); },
diamond: function() { return render_vector_ngon(4, xr, yr, offset); },
square: function() { return "" },
triangle: function() { return render_vector_ngon(3, xr, yr, offset); },
star: function() { return render_vector_star(5, a.w, a.h, a.stroke); },
burst: function() { return render_vector_star(10, a.w, a.h, a.stroke); },
speechbubble: function() { return render_vector_speechbubble(xr, yr, offset); },
heart: function() { return render_vector_heart(xr, yr, offset); },
cloud: function() { return render_vector_cloud(xr, yr, offset); },
}
var render_func = shape_renderers[a.shape];
if (!render_func) return "";
return render_func();
}
UPDATE: My fix for the stars problem was accepted on July 23, 2020… my first ever contribution to a public open-source software project!!!
Problem Two: Adding Fonts to the Space
This was an easy one to fix. It was really a documentation fix. So, I wrote a bit of documentation for Spacedeck-open and it was accepted.
Problem Three: Other Users’ Cursors Don’t Display in the Correct Location
This was a bit bigger problem: cursor positions on shared whiteboards are inconsistent. It took me quite a while to fully debug it. In some ways it was quite simple: basically, the translation from absolute window coordinates to the coordinates of the virtual space was not being done correctly.
There were a few minor dependencies on the _incorrect_ calculations so I had to fix those references as well.
The key changes are in the file public/javascripts/spacedeck_whiteboard.js in the cursor_point_to_space method. The original version of the method looks like this:
cursor_point_to_space: function(evt) {
var $scope = this.vm.$root;
var offset = {left: 0, top: 0};
evt = fixup_touches(evt);
return {
x: (parseInt(evt.pageX) - parseInt(offset.left) - $scope.bounds_margin_horiz) / this.space_zoom,
y: (parseInt(evt.pageY) - parseInt(offset.top) - $scope.bounds_margin_vert) / this.space_zoom
};
},
After changes it looks like this… pretty similar, really:
cursor_point_to_space: function(evt) {
var $scope = this.vm.$root;
evt = fixup_touches(evt);
return {
x: $scope.scroll_left + (parseInt(evt.pageX) - $scope.bounds_margin_horiz) / $scope.viewport_zoom,
y: $scope.scroll_top + (parseInt(evt.pageY) - $scope.bounds_margin_vert) / $scope.viewport_zoom
};
},
Basically, the zoom info wasn’t being obtained from the correct place and the scroll offset was being ignored.
There were actually a bunch of other places in that file that needed to be changed because there were 12 references to the method. There was another method also used called offset_point_in_wrapper that was related, but I removed the need for it and deleted the method. And finally, there was a small change to the html related to the whiteboard to put the “lasso” div in the same frame of reference as all the objects on the whiteboard so that it didn’t need any special calculation handling for mouse coordinates.
I’ve manually tested the results, and I think they’re good, but since there aren’t any automated tests, I’m a little leery of submitting my work… oh well.